HTR subsets解説 〜DRからHTRを作るために〜
こんにちは、うえしゅうです。
FMCの解法、Domino Reduction(DR)ではHalf Turn Reduction(HTR)という工程があります。
このHTRを作る上で覚えておくと役立つHTR subsetsという手法をこの記事では説明します。
注意:この記事ではDRに関する詳しい説明は行いません。DRについて学びたい方は以下のリンクを参照ください。
HTR subsetsの概要
HTRとは?
HTRとは、DR状態から[U2, D2, R2, L2, F2, B2]といったHalf Turn(HT)のみで揃えられる状態に持っていくステップのことを言います。 見た目としては、UD面が白か黄色の2色、RL面が赤かオレンジの2色、FB面が緑か青の2色になっています。
注意しておきたいのは、上記のようにそれぞれの対面が2色になっていたとしてもHTRだとは限らないということです。 例えばNa permは全ての対面が2色になっていますが、これはHTのみでは揃えられません。 コーナーの位置関係を意識しつつ対面を2色にしないといけないんですね。
HTRを行うとその後のFinishまでが比較的短くなることが多いです。
HTR subsetsとは?
HTRを作る上で重要なのがQTという考え方です。
簡単に言うと、あるDR状態からHTRを作るにはそのDR状態が何回90度回転(Quarter Turn, QT)をすればHTR状態に持ち込めるかを判別し、その回数だけ適切にQTを回すことが必要になります。
HTR的にはあるDR状態からどれだけHTを回してもそのDRのHTR的状態は変わりません。 しかし、一度QTを回すとHTR的状態が変わり、HTR完成に状態が近づくか遠ざかるかするのです。
このQTという考え方を元にDR状態をHTR的観点から14個のパターンに分類したものをHTR subsetsと呼びます。
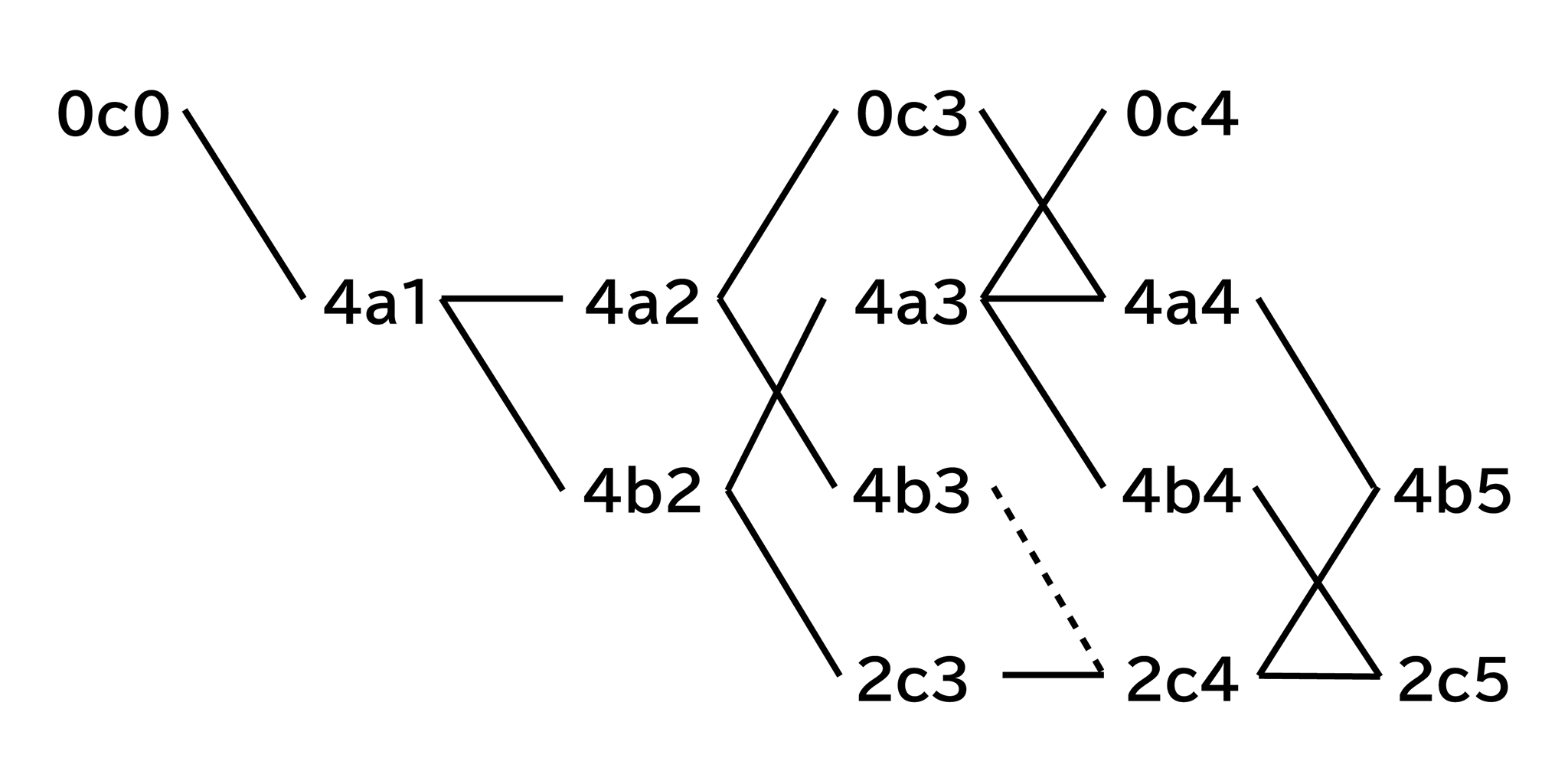
各subsetは以下の樹形図のそれぞれの項目に対応し、適切な位置でQTを回すと必要QT数が減り次のsubsetに遷移するのです。
最終的に0c0に遷移したらコーナーのHTRが完成します。
このHTR subsetsはFMCの元WR holderのJayden McNeilが提唱したもので、以下にその元記事と解説YouTubeを載せておきます。
FMC: My recommended approach for recognizing all 12 HTR corner subsets
HTR subset recognition tutorial (YouTube)
これら元記事を見てもらえば僕の記事は見る必要全く無いんですが、英語はわからん!という人のためにこの記事では日本語でHTR subsetsを解説します。
HTR subsetsの種類
bad cornerという考え方
HTR subsetsを知る上で、まずはbad cornerという考え方を知っておく必要があります。
以下のスクランブルを回してみてください。このスクランブルはUD面のDRがすでに揃っています。
スクランブル: U F2 U
コーナーだけに着目します。
それぞれのコーナーがHTだけで正位置に戻れるか試してみてください。
例えばUFRコーナーはU2で正位置に戻るためgood cornerです
また、UFLコーナーはF2 D’で正位置に戻るため、HTだけでは正位置に戻らずQTが必ず必要になります。そのためこれはbad cornerです。
このgood corner、bad cornerはもっと簡単な判別方法があります。
例えばUFRコーナーはF面のFURステッカーとF面センターとが対面色です。 このように側面ステッカーと側面センターが同色または対面色の場合、それはgood cornerです。
また、UFLコーナーはF面のFULステッカーとF面センターとが隣接色になっています。 このように側面ステッカーと側面センターが隣接色の場合、それはbad cornerです。
これらを踏まえてこのスクランブルのbad cornerの位置を確認すると、UFL, UBL, DFR, DFLであることがわかります。
このbad cornerの個数と位置情報を使ってパターンを判断します。
コーナーの種類
bad cornerの状態は以下の4パターンあり、それぞれ以下のように名前付けがされています。
| bad cornerの個数 | 位置関係 | 名称 |
|---|---|---|
| 0個 |  | 0c |
| 2個 |    | 2c |
| 4個 |     | 4a |
| 4個 |   | 4b |
まずbad corner0個は確定で0cです。
次にbad corner2個はこれも確定で2cです。 表にあるように位置関係が3パターンありますが、個数だけで判別できるのでそんなに難しくないです。
次にbad cornerが4個の場合、位置関係によって2つの状態のどちらかに分岐します。
もしその4コーナーがHTによってUD面に集められるのであれば、それは4aです。 4aは位置関係が4パターンあり、UD面に全て集まっているもの、U面に隣接2個かつD面の対角線上に隣接2個、側面に全て集まっているもの、UD面それぞれ対角2個、の4パターンです。
もしその4コーナーがHTによってUD面に集められないのであれば、それは4bです。 4aは位置関係が2パターンあり、U面に隣接2個かつD面に隣接2個かつそれらが隣接面、UD面にそれぞれ1個と3個、の2パターンです。
これでコーナーの状態が特定できたため、最後にそれぞれのパターンにおける可能なQT数を列挙します
| コーナーの状態 | QT数 | パターン名 |
|---|---|---|
| 0c | 0 | 0c0 |
| 3 | 0c3 | |
| 4 | 0c4 | |
| 2c | 3 | 2c3 |
| 4 | 2c4 | |
| 5 | 2c5 | |
| 4a | 1 | 4a1 |
| 2 | 4a2 | |
| 3 | 4a3 | |
| 4 | 4a4 | |
| 4b | 2 | 4b2 |
| 3 | 4b3 | |
| 4 | 4b4 | |
| 5 | 4b5 |
この0c3や2c5といった名前がHTR subsetsにおける各パターンの名称になります。
おわかりかとは思いますが、この4b2のような名前は「4b(コーナーの個数と位置関係) + 2(QT数)」を表しています。
表にまとめた通り、HTR subsetsは全部で14個あります。
判断方法
次はDR状態からHTR subsetsのパターンを判別する判断方法を説明します。
0c, 2cの判別方法
0cと2cの判断方法は、凛さんの記事でわかりやすく解説されています。
概要だけ言うと、0cの場合は以下の通りです。
- 揃っている軸/揃っていない軸の判断基準を覚える
- U/D面、R/L面、F/B面それぞれについて、軸が揃っているかを判断する
- 揃っている軸の個数でsubsetが確定する (0個→0c4、1個→0c3、3個→0c0)
2cの場合は以下の通りです。
- 2つのbad cornerの位置を入れ替えた状態を頭の中で想像する。
- 入れ替えた状態で、U/D面、R/L面、F/B面それぞれについて、軸が揃っているかを判断する
- 揃っている軸の個数でsubsetが確定する (0個→2c3、1個→2c4、3個→2c5)
4a, 4bの判別方法
4aと4bの判断方法は2ステップあり、1ステップ目はNISSトレース、2ステップ目はBLDトレースです。
BLDトレースとは、3BLDのようにバッファからパーツを分析していき分析文字列が奇数か偶数かを判別するというものです。 この際3BLDのように文字化する必要はなく、単に分析結果が奇数か偶数かがわかればいいので簡単です。
NISSトレースとは、bad cornerがそれぞれNISSした後にどの位置関係になるかを予測する手法です。
説明が難しいのですが、ここではとても簡単なNISSトレースの判断方法をお教えします。
スクランブル: R2 U' R2 U R2 U2 F2 U'
bad cornerはUFR, UBR, DFR, DBRです。
それぞれのbad cornerのUD面色を見ると、黄色、黄色、黄色、白となっています。
bad cornerのUD面色にどちらかの色が3個含まれていたら、その状態はNISSした時に4bの位置関係になります。
スクランブル: U' R2 U R2 U2 F2 U'
bad cornerはUFR, UBR, DFR, DBRです。
それぞれのbad cornerのUD面色を見ると、白、黄色、白、黄色となっており、2個+2個なのでこの時点ではNISS後に4aになるか4bになるかはわかりません。
次にbad cornerのどちらかの側面色を見ましょう。 今回は青と緑の面を見ることにします。
bad cornerの側面色はそれぞれ青、緑、緑、緑となっています。
bad cornerの側面色にどちらかの色が3個含まれていたら、その状態はNISSした時に4bの位置関係になります。
スクランブル: U R2 U2 F2 U' F2 U'
bad cornerはUFR, UFL, DFR, DBRです。
それぞれのbad cornerのUD面色を見ると、白、黄色、黄色、白となっており、2個+2個なのでこの時点ではNISS後に4aになるか4bになるかはわかりません。
続いてbad cornerの側面色(青、緑)はそれぞれ緑、緑、青、青となっており、これも2個+2個のため、これはNISSした時に4aの位置関係になります。
このNISSトレースとBLDトレースを使うと、以下の表のようにパターンを特定できます。
| 現在の状態 | NISSトレース | BLDトレース | QT数 | パターン名 |
|---|---|---|---|---|
| 4a | 4a | 奇数 | 1 | 4a1 |
| 4a | 4a | 偶数 | 2 | 4a2 |
| 4b | 4b | 奇数 | 5 | 4b5 |
| 4b | 4b | 偶数 | 2 | 4b2 |
| 4a | 4b | 奇数 | 3 | 4a3 |
| 4a | 4b | 偶数 | 4 | 4a4 |
| 4b | 4a | 奇数 | 3 | 4b3 |
| 4b | 4a | 偶数 | 4 | 4b4 |
4aと4bの特徴として、4a3はNISSすると4b3となり、4a4はNISSすると4b4となるというものがあります。 つまり4a3と4b3、4a4と4b4はHTR的には実質同じパターンというわけです。
ちなみに上記の4a3, 4b3, 4a4, 4b4以外のHTR subsetsは、NISSしても変わらず同じパターンになります。(4b2はNISSしても4b2のまま)
それぞれのsubsetに対しての取り組み方
ここからはそれぞれのHTR subsetsのパターンに対してどう取り組めばQT数が減るかを解説していきます。
0c0
すでにコーナーがHTR状態になっています。 エッジも全てHTR的に揃っているなら完成です。
もしエッジがいくつか揃っていない場合、一度QTを回して4a1 4e4cにしてから解くといいでしょう。
U R2 L2 DというHTRトリガーが有用です。
0c3
bad caseなので、基本的には捨てたほうがいいです。
もしやるとしたら、QTを回すと4a2か4a4のどちらかになるため、4a2になるようにコーナーを調節しましょう。
0c4
bad caseなので、基本的には捨てたほうがいいです。
もしやるとしたら、U R2 Uトリガーを回すと4b2か4b4となるため、4b2になるようにコーナーを調節しましょう。
4a1
4e4cであればセットアップして解くことが可能です。R2 F2 R2 UなどのHTRトリガーが有用です。
4e4cでない場合、確実に+2qt必要になるので一度QTを回して4b2か4a2に持ち込んでから取り組みましょう。
4a2
 → QTを回す →
→ QTを回す → 
上記画像のように、bad cornerを両方スラッシュの形にセットアップしてからQTを回すと同じ4aのままQTが1減ります。 4aから4aへの遷移はこのスラッシュケースしかないため、覚えておくといいでしょう。
4a1にする時ちゃんと4e4cにしないと1qtで解けないことに注意!
4b2
2e4cならU' R2 U、4e4cならU R2 F2 UといったHTRトリガーが使えます。
正直この4b2が一番取り組みやすいです。
ちなみに4b2には普通にHTRトリガーを回してもFake HTRとなるケースが存在するため、その対処方法を説明します。
スクランブル: U' L2 U L2 U2 F2
見たところU F2 U’のHTRトリガーでHTRが揃いそうに見えますが、これではFake HTRとなってしまいます。
こういう時はまずF2でbad corner3つを片方の面(ここではU面)に集め、U2でその面をHT回します。 そしてL2すると後ろでU' L2 UのHTRトリガーが使えるようになり、これで真のHTRが作れます。
手順としては、bad corner3つ集める→U2する→bad cornerを2個2個にする、でFake HTRからTrue HTRへの移行が可能です。
4a3
3qtの中ではそんなに良くないケースです。
方法としては、bad cornerをUD面それぞれ隣接2つの形にしてQTを回すと4b2または4b4になります。 4b4になってしまうケースが厄介なのですが、先述のNISSトレースを使えば4b2か4b4かの判別ができます。 4b4になってしまう場合、QTの前にHTを入れてみると4b2になる可能性が高いです。
4b3
bad cornerをUD面それぞれ隣接2つの形にしてQTを回すと必ず4a2になります。
4a4
bad caseなので、基本的には捨てたほうがいいです。
もしやるとしたら、4a2 -> 4a1の時のようにbad cornerを両方スラッシュの形に置いてからQTを回すと必ず4a3となるため、このルートがいいでしょう。
 → QTを回す →
→ QTを回す → 
4b4
bad caseなので、基本的には捨てたほうがいいです。
もしやるとしたら、 下記画像のようなU' R2 UでFake HTRとなる配置にbad cornerを置いた時に、逆にU R2 U’と回すと4b2となるため、このルートがいいでしょう。

4b5
bad caseなので、基本的には捨てたほうがいいです。
もしやるとしたら、bad cornerを同じ面に3つ集めてQTを回すと必ず2c4になるため、このルートがいいでしょう。
2c3
2つのbad cornerを片方U面片方D面に分離してQTを回すと必ず4b2になります。
UD面に分離した状態でどれだけHTを回してもQT回すことで必ず4b2になるので、色んな4b2が作れてお得です。
3qtの中でこの2c3が一番取り組みやすいケースだと思います。
2c4
2つのbad cornerを同じ面に持っていきQTを回すと2c3か2c5になります。
2c3か2c5かを判別するには先述の方法を使ってください。
4qtの中では比較的扱いやすいケースです。
2c5
bad caseなので、基本的には捨てたほうがいいです。
もしやるとしたら、bad cornerを同じ面に集めてQTを回すと必ず2c4となるため、このルートがいいでしょう。
実践例
スクランブル: B2 U R2 U2 L2 R2 F2 B2 U R2 L2 U2 B2 U B2 U L2 U2 R2 U' R2 U' L2 U2 L2
まず、bad cornerはUFR, UBR, UBL, DBLの4つです。
そしてこの位置関係は4bの位置関係になります。
次に4bの場合、NISSトレースを行います。
bad cornerの白黄面はそれぞれ黄色、白、黄色、白で、この時点では4aか4bかわかりません。
続いて青緑面を見ると、それぞれ青、青、緑、緑となり、NISSトレースの結果4aとわかりました。
続いてBLDトレースをすると偶数でした。
これらの結果を総合すると、4bの状態、NISSトレースで4a、BLDトレースで偶数のため、このDRの状態は4b4とわかりました。
4b4は捨てなので、取り組まなくていいことがわかります。
もしやるのであれば、F2でbad cornerをU/D面に2つずつにし、U' L2 UでFake HTRができるところを逆にU L2 U’と回すことで4b2となり、そのまま続けることができます。
スクランブル: U2 F2 U' L2 U F2 L2 U' L2 U' B2 U' B2 U2 L2 U' F2 B2 L2 F2 U L2 R2 B2 L2
まず、bad cornerはUBR, DBRの2つです。
2cなので、2つのbad cornerを入れ替えた状態を頭の中で想像します。
入れ替えた状態での各軸の状態は以下の通り。
- U/D軸: 各色のbarが垂直となっているため、軸は揃っていない
- R/L軸: 各色のbarが垂直となっているため、軸は揃っていない
- F/B軸: 各色のbarが垂直となっているため、軸は揃っていない
よって揃っている軸は0個だったため、このDRの状態は2c3とわかりました。
2c3なので対面にbad cornerを置いてQTを回します。 この場合すでに対面にbad cornerがあるので、Dを回すことで4b2 2e4cにします。
badパーツの位置を見ると、R2すればU F2 U’でHTRができそうな気がしますが、回してみるとこれはFake HTRでした。
こういう時はUD面にbad cornerを3つ集めてHT回すんでしたね。
初期状態からDを回した状態はD面にbad cornerが3つ集まっているため、ここからD2をしてbad cornerの位置を変え、B2するとU' L2 Uで真のHTRが引けました。
まとめると解法は以下のようになります。
D' B2 U' L2 U // HTR
終わりに
HTR subsetsはHyper-Parityと比べればパターン数も半分以下でわりかし習得しやすい方法なんじゃないかと思っています。
これに慣れ親しめば少なくともコーナーは手順を知ることなく揃えることができます。
HTRを作るという観点でいうと、この考え方にプラスしてエッジの位置関係を考える必要があるので、実際にはHTR subsetsだけではHTRはマスターしたことにはなりません。 ただHTRを作るにあたっては、まず4b2や4a1にコーナーの状態を持っていき、そこからU R2 UなどのHTRトリガーにセットアップするという手法で大半は作ることができると思います。
HTR subsetsを学んであなたもHTRの世界に足を踏み入れよう!