DR初心者が回答を書けるようになるためには
こんにちは、うえしゅうです。
FMCの解法であるDR(Domino Reduction)はとても優秀な解法で昨今のFMCの主流となっているのですが、学ぶべきことが多く初心者にはハードルの高いものとなっています。
この記事では、初心者がまずはDRの回答を1つ書けるようになるために必要な最低限の情報を順序立てて説明します。
また、最後にその方法で解いたときの実践例を1つ載せておきます。
DRの各ステップにおける取り組み方
DRは以下のステップで行われます。各ステップの概略と、何を学べばよいかの解説を行います。
EO -> RZP -> DR -> HTR ( -> FR ) -> Leave Slice -> スライスインサート
EO
EOとは、各エッジの向きをすべて合わせるステップです。
いかのおすしさんのこちらの記事を読めば、EOの概略とその解き方が把握できると思います。
EOにおける初心者へのtipsは以下の通りです。
- EOは5手以内のものを探しましょう。1ソルブでだいたい3〜5個見つけられたら十分かなと思います。
- EOはFB軸のものを探せればそれで十分ですが、5手以内のEOが極端に少ないときもあったりするので、LR軸のEOも探せればベストです(必須ではない)。
- bad edgeの個数ごとのEOの解き方
- bad edgeが4個: [U, D, R, L, F2, B2]を使ってF/B面に4つ集めてF/B
- bad edgeが8個: まず4つF/B面に集めてF/B、そして残りの4つをF/B面に集めてF/B
- bad edgeが2個: bad edgeを1つだけF/B面に置いてF/Bするとその面のbad edgeが3つになる。これでbad edgeが計4つになるので、F/B面に集めてF/B
- bad edgeが6個: bad edgeを3つだけF/B面に置いてF/Bするとその面のbad edgeが1つになる。これでbad edgeが計4つになるので、F/B面に集めてF/B
RZP
RZPとは、EO後に数手回すことでDRにおけるbadパーツの個数をDRトリガーのbadパーツの個数と同じにするステップです。
RZPのより詳細な概要、RZPの見つけ方についてはこちらの記事をご覧ください。
RZPにおける初心者へのtipsは以下の通りです。
- EO+RZPの手数は初心者には6手以内を推奨します。
- FB軸EOからはUD面DRの他にRL面DRも作ることができます。そのためRL面DR用のRZPも見逃さないようにしましょう。zしてRL面がUDになるように持ち替えてから探すと探しやすいです。
DR
DRとは、U/D面がU/D面色で統一されておりE列がE列パーツのみである状態を指します。
RZPからDRを作るまでのステップについてはこちらの記事で学習するとコツが分かります。
RZPからDRを作る例 5選 - uesyuu’s Blog
DRにおける初心者へのtipsは以下の通りです。
- RZPからDRを作るまでのステップは、初心者は手数をかけてもいいステップであると個人的には思います。なぜなら、初心者は探せるEOや見つかるRZPの数が少なく、その少ないRZPの中でやりくりしなければならないからです。DRペアが1つでもあれば、先ほどの記事を参考にDRトリガーの形を目指してみましょう。
- 逆に、DRペアが1つもなければさすがにそのRZPは捨てでいいと思います。
HTR
HTRとは、すべての面が同面色と対面色の2色で構成されていて、かつHalf Turnで揃えることが可能な状態を指します。
エッジを無視したコーナーのみのHTRを作るための方法はこちらの記事で解説しています。
HTR subsets解説 〜DRからHTRを作るために〜 - uesyuu’s Blog
HTRにおける初心者へのtipsは以下の通りです。
- 初心者がHTR状態を作る一番楽な方法は、HTR subsetsを使いコーナーのみのHTRを作成したあとにエッジのHTRを完成させる、というようにコーナーとエッジを独立させて解くことだと思います。コーナーHTR後、だいたい4〜8手でエッジHTRも揃えることができます。
- コーナーHTR後、bad edgeの個数は0個、2個、4個、6個、8個のどれかになります。それぞれどう解くかを解説します。
- 0個: すでにHTRが完成しています。
- 2個: UR, DFにbad edgeを置いて
U R2 F2 R2 UでHTR完成となります。Uでbad edgeを縦に並べるイメージです。 - 4個: UR, UL, DF, DBにbad edgeを置いて
U R2 L2 DでHTR完成となります。Uでbad edgeをすべてM列に並べるイメージです。 - 6個: 上記方法で4個のbad edgeを消したあと、2個のbad edgeを消す感じです。
- 8個: 上記方法で4個を消し、また4個を消すといった感じです。
FR
FRとは、HTR後に特定の操作をすることで[R2, L2, F2, B2]のみでU/D面を揃えられる状態にするステップです。
HTR後に直接U/D面を揃えられればこのステップはいらないのですが、それは結構難しいので初心者にはこのFRを経由するのをおすすめします。
FRの作り方はいかのおすしさんのこちらの記事で詳しく解説されています。
FR(Floppy Reduction)解説 - いかのおすし
Leave Slice
Leave Sliceとは、E列パーツ以外すべて揃っている、つまりU/D面のパーツがすべて揃っている状態です。ちなみにこの時点でE列パーツも揃っている可能性があり、その場合ここでステップ終了です。
FR後は必ず8手以内でこのLeave Sliceの状態にすることができます。
FRからLeave Sliceのステップは3x3が解ける人であれば特に難しくないので、[R2, L2, F2, B2]を色々回していれば難なく揃えられると思います。
スライスインサート
Leave Sliceの状態で揃っていないのはE列パーツのみです。
スライスインサートとは、DR -> HTR -> FR -> Leave Sliceまでの解法の中にあるU/D回転を二層回しにしたり途中にE回転を挟んだりすることで、手数をほとんど増やすことなく完成状態に持っていくことができる手法です。
スライスインサートはShotaさんのこちらの動画で詳しく解説されています。
スライスインサートはもちろん使うと手数を大幅に削減できるのですが、DR初心者には個人的にはおすすめしません。なぜなら、すでにここまで大量に覚えることがあって大変だというのと、スライスインサートを使わなくてもDRの回答自体は書けるということです。
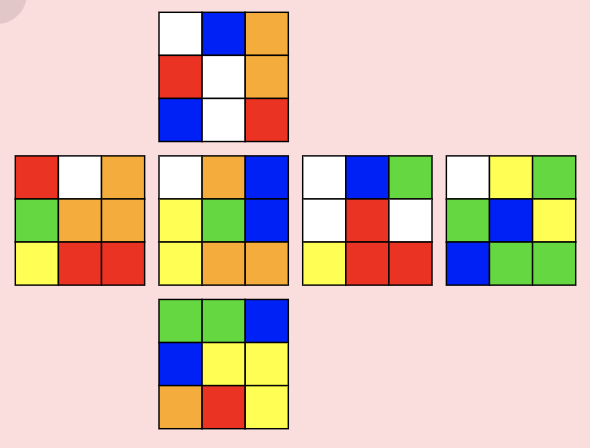
Leave Sliceの時点でE列の状態は以下の4つの状態のうちのどれかになっています。それぞれの状態の解き方を載せておきます。
| E列が揃っている | E列が3点交換 | E列が並行交換 | E列が対角交換 |
|---|---|---|---|
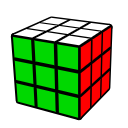 | 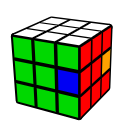 | 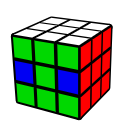 | 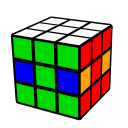 |
| R2 E R2 E' | R2 E2 R2 E2 | R2 L2 E R2 L2 E' |
この3つの手順を覚えることでDRの回答を書き下すことができます。お疲れ様でした。
ただこの手順を使うと6〜8手ほどプラスされてしまうので、まだ余力がある方はスライスインサートを学んでみても良いと思います。
また、これら手順はFRの最後とキャンセルする可能性があります。時間に余裕があればそちらを探してみるのもいいでしょう。
実践例
ここからは、実際のスクランブルを使って上記方法でDRの回答を作っていきます。
Scramble: R' U' F U R2 F' L2 U2 B' L2 B F2 D2 R2 U F U2 B2 R U' B2 F R' U' F
EO
FB軸EOのEOパーツを探してみましょう。F面にはFR、S列にはURとUL、B面にはUBとBRとDBがEOとなっています。このように、F面、S列、B面と分けてEOを把握すると、どのエッジをF/B面に集めればいいかが把握しやすくなります。
EOは6個でした。つまり3個をF/B面に集めてF/Bする必要があります。先程見たようにB面にすでに3個固まっていたので、B or B’することでEOが4個になります。
Bしたとき、EOはFR, UR, UL, DBです。F面に1つすでに入っているので、4つすべてF面に集めることを考えます。
まずUしてURをF面に入れようと考えますが、そうするとULがL列から逃げてしまい、FLにEOパーツを入れにくくなってしまうのでこれは却下。
次にLしてULをF面に入れようとします。これは他のEOパーツに干渉しないのでいいですね。URをUして入れ、DBをD2して入れることで、すべてのEOパーツがF面に集まりました。最後にFしてEO終了です。
Solution: B L U D2 F // EO ①
他にもEO解法を探してみましょう。DBをD2でF面に入れる動作も他のEOパーツに干渉しません。ULをLで入れ、URをUで入れることで、すべてのEOパーツがF面に集まりました。最後にFしてEO終了です。
Solution: B D2 L U F // EO ②
RZP
EOが2つ見つかったので次はRZPを探してみましょう。EO+RZPは6手にしてみます。そのためこの5手EOで見るべきなのは0手RZPと1手RZPです。
まず0手RZP。①の方でRL面にDR-4e4cのRZPがすでにできている事がわかります。他にはありませんでした。
続いて1手RZP。R, L, U, Dと、F2してR, L, U, Dするんでしたね。残念ながら1手RZPはどちらのEOにもありませんでした。
Solution: B L U D2 F // EO, RZP(DR-4e4c)
DR
続いて、見つかった1つのRZPからDRを作りに行きます。
RL面なのでz持ち替えして確認するとbadパーツの把握がしやすいです。ただ、これから説明するときの回転記号やパーツの位置は持ち替えなしの白U緑Fで説明するので、適宜変換しながら読んでください。
UFL-FL-DFLにすでにDRバーがありますね。とてもいい。しかしUBLとDBLにCOが同じ方向を向いたコーナーがあります。これはとても悪い。とりあえずB2してUBR-URにDRペアを作ります。
ここからF2するとDRバーとDRペアが直角に並ぶいい形になるのですが、残りのコーナーがDBRにあり、すべてのbadパーツがR面に配置されています。これはめちゃくちゃ悪いパターンです。何としてでも回避しなければなりません。
一旦DRペアとDBRコーナーを分離してから考え直してみましょう。分離する方法はR' F2とL' U2の2パターンありますが、M列の bad edgeが今UFとUBで対面を向いておりとてもいい状態なので、この状態を壊さないためにL' U2を選択します。
そしてもう一度DRバーとDRペアの直角を作りに行きます。R B2とL U2の2パターンありますが、もちろんM列の位置関係を保存するためにL U2を選択。
DRに近づいてきましたね。次は残りのDBRコーナーをDRペアにくっつけてDRバーにするためにR' U2と回します。そしてL’と回すとすべてのbadパーツがU面に集まりました。UをしてDRが完成です。
Solution:
B L U D2 F // EO, RZP(DR-4e4c)
B2 L' U2 L U2 R' U2 L' U // DR
HTR(コーナー)
DRができたので、次は今の状態がHTR subsetsにおけるどの状態か特定します。
bad cornerはUFR, DFR, UFL, UBLの4つ、そしてこの4つの配置はHalf TurnのみでR/L面に集められないため4bであるとわかりました。
4a, 4bの場合NISSトレースとBLDトレースをするのでしたね。
まずはNISSトレース。bad cornerのR/L面を見ると、それぞれ赤、オレンジ、オレンジ、オレンジでした。同じ色が3個あったのでNISS後は4bになるとわかります。
次はBLDトレース。文字数を数えてください。文字数は6文字、つまり偶数でした。
現在4bでありNISS後も4b、コーナーの偶奇は偶数、つまりこのDRのコーナー状態は4b2で確定です。
4b2ならばR/L面にそれぞれ2つずつ置いてR U2 Rトリガーが使えます。ちょうど今それが使える配置になっています。R U2 Rを回してみてください、どうなったでしょうか。R面にオレンジコーナーが3つあります。そうです、この状態はFake HTRなのです。一旦R U2 Rと回したのを元に戻してください。
4b2でFake HTRを回避するには、R/L面にbad cornerを3つ置いてその面をHalf Turnさせるのでした。今の状態からU2するとR面にbad cornerが3つ集まりますね。ここでR2することでFake HTRから真のHTRへ切り替わりました。
最後の仕上げです。HTRトリガーの状態に持っていくためにB2してbad cornerをR/L面に2つずつにします。最後にHTRトリガーのR' B2 Rを回すことでコーナーHTRが完成しました。これはFakeではない真のHTRです。
Solution:
B L U D2 F // EO, RZP(DR-4e4c)
B2 L' U2 L U2 R' U2 L' U // DR
U2 R2 B2 R' B2 R // corner HTR
HTR(エッジ)
コーナーHTRができたので、次はエッジHTRを行い完全なHTRを目指します。
bad edgeはUR, FR, FL, DLの4つです。4つなのでU R2 L2 Dトリガーの形を目指します。U R2 L2 Dトリガーの形というのは、各DR面にそれぞれbad edgeが対面に並んでいる配置です。
まずU2してUL-DLの対面bad edgeを作ります。続いてR2 F2することでFR-BRのの対面bad edgeを作ります。最後にトリガーであるR F2 B2 Lを回せばエッジHTRが完成、つまり完全なHTRが完成です。
Solution:
B L U D2 F // EO, RZP(DR-4e4c)
B2 L' U2 L U2 R' U2 L' U // DR
U2 R2 B2 R' B2 R // corner HTR
U2 R2 F2 R F2 B2 L // HTR
FR
続いてFRのステップです。FRはまずコーナー4つの置換と中列エッジの置換から全体の偶奇を判定し、U2の回数を特定するのでしたね。
コーナー4つの置換(UBL, UFR, DFL, DBR)はUBL-UFRのみが交換されているので、偶奇は奇数です。
中列エッジの置換(UF, DF, UB, DB)は4点交換となっているので、偶奇は奇数です。
よって奇数+奇数のため全体の偶奇は偶数となり、U2は0回か2回です。しかし今のRL面の状態はFR状態となっていないため、0U2ではありません。つまりこの時点でU2が2回、2U2が確定しました。
次にFRを解いていきます。
bad edgeはFR, UR, BR, FL, DL, BLの6つです。6つなのでまずは4つにしていきます。R2するとbad edgeは4つになりますが。コーナーペア(UFR-UFL)が揃ってしまいます。これは1U2ではないためR2は却下。
F2でbad edgeの位置を変えてからR2してみます。するとコーナーペアが揃わずにbad edgeが4つとなりました。これで1U2完成です。
次に0U2にしていきます。U2するとbad edgeがL面に4つ集まるのですが、L2してみてもコーナーペアは完成しません。却下。
こういうときの方法は2パターンあります。一つはF2して一旦1つL面からbad edgeを出してからU2 F2と順々に入れて最後L2する方法です。しかしこれでもコーナーペアは揃いませんでした。
2つ目の方法は、一旦U2してすべてL面に集めてからF2 U2と順々にbad edgeを出し、F2 U2といったようにさっきとは逆順にエッジを入れて最後L2する方法です。この方法で無事コーナーペアが揃い、FRが完成しました!
FRの1U2状態における最後1つのbad edgeの入れ方は上記の3通りしかなく、そのどれかをやれば必ずFRは完成します。
Solution:
B L U D2 F // EO, RZP(DR-4e4c)
B2 L' U2 L U2 R' U2 L' U // DR
U2 R2 B2 R' B2 R // corner HTR
U2 R2 F2 R F2 B2 L // HTR
F2 R2 U2 F2 U2 F2 U2 L2 // FR
Leave Slice
ここまで来ればあとはもう近いです。B2 U2 F2と回してみましょう。R/L面が完成することがわかります。
Solution:
B L U D2 F // EO, RZP(DR-4e4c)
B2 L' U2 L U2 R' U2 L' U // DR
U2 R2 B2 R' B2 R // corner HTR
U2 R2 F2 R F2 B2 L // HTR
F2 R2 U2 F2 U2 F2 U2 L2 // FR
B2 U2 F2 // Leave Slice
残りM列(スライスインサートは無し)
現在の状態はM列エッジの3点交換となっています。3点交換の場合は6手の手順を回すんでしたね。U2 M' U2 Mと回すことでキューブが完成します。FMCではスライスムーブは禁止なので、きちんとU2 R' L F2 R L’と書きましょう。
Solution:
B L U D2 F // EO, RZP(DR-4e4c)
B2 L' U2 L U2 R' U2 L' U // DR
U2 R2 B2 R' B2 R // corner HTR
U2 R2 F2 R F2 B2 L // HTR
F2 R2 U2 F2 U2 F2 U2 L2 // FR
B2 U2 F2 // Leave Slice
U2 R' L F2 R L' // Finish (43 moves)
これでDR回答が完成です!!!お疲れ様でした。
おわりに
少し長くなってしまいましたが、この記事を読めば確実にDRの回答が書けるようになるのではないかと確信しています。
DRで回答を作るための最低限の知識をすべて盛り込んだつもりです。
もしこれを読んでわからなかった箇所があれば、@uesyuu_cubeまでコメントください、いつでも対応します。
これを読んでより多くの皆さんがDRで回答を作れるようになることを願っています。
それでは。